如何理解普通年金與預付年金的終值和現值轉換關系
怎么理解普通年金終值→預付年金終值,是期數+1
普通年金現值→預付年金現值,是期數-1
請老師說的簡單點!謝謝
問題來源:
【例題?單選題】假設銀行利率為i,從現在開始每年年末存款1元,n年后的本利和為[(1+i)n-1]/i元。如果改為每年年初存款,存款期數不變,n年后的本例和應為( )元。(2014年)
A.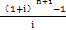
B.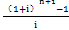 -1
-1
C.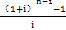 +1
+1
D.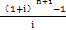 +1
+1
【答案】B
【解析】預付現金終值系數和普通年金終值系數相比,期數加1,系數減1。

樊老師
2020-08-15 16:17:13 8133人瀏覽
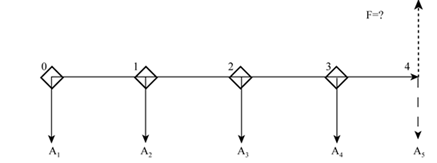
預付年金終值是一定時期內,將按相同的時間間隔每期期初收付的相等金額折算到最后一期期末的終值合計,也就是說第一個年金發生在第一期期初,即0時點(如圖A1),第二個年金發生在第二期期初即第一期期末,即1時點(如圖A2),依此類推,根據圖示可知:
如把A1看做發生在第0年年末,那么在第四期期末補充一個A5,就構成了一個五期的普通年金形式,求解該年金的終值為A×(F/A,i,5),A5發生在最后一期期末,實際不存在,所以四期的預付年金終值為A×(F/A,i,5)-A,即A×[(F/A,i,5)-1],由此可知預付年金終值系數是在普通年金終值系數的基礎上期數加一,系數減一,即預付年金終值F=A×[(F/A,i,n+1)-1]。
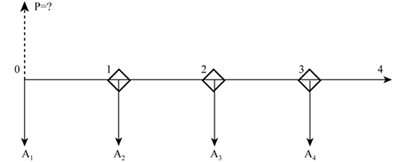
預付年金現值是一定時期內,將按相同的時間間隔每期期初收付的相等金額折算到第一期期初的現值合計,也就是說第一個年金發生在第一期期初,即0時點(如圖A1),第二個年金發生在第二期期初即第一期期末,即1時點(如圖A2),依此類推,根據圖示可知:
如不考慮A1,那么A2至A4構成了三期的普通年金,求解0時點現值為A×(P/A,i,3)。考慮A1,A1發生在0時點,不需要進行折現,即四期的預付年金現值為A×(P/A,i,3)+A,即A×[(P/A,i,3)+1],由此可知預付年金現值系數是在普通年金現值系數的基礎上期數減一,系數加一,即預付年金現值P=A×[(P/A,i,n-1)+1]。
您看您可以理解么?若您還有疑問,歡迎提問,我們繼續討論,加油~~~~~~~~~~~相關答疑
-
2025-06-15
-
2025-06-15
-
2025-03-21
-
2025-03-15
-
2025-03-11
您可能感興趣的CPA試題









 津公網安備12010202000755號
津公網安備12010202000755號