相關(guān)系數(shù)=1時，為什么組合不能抵消任何風險？
1：相關(guān)系數(shù)=1，為什么組合不能抵消任何風險，還是不太明白。麻煩老師詳細說一下
問題來源：
5.N種股票的組合風險衡量
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
N |
||
|
1 |
11 |
|||||||||
|
2 |
22 |
|||||||||
|
3 |
33 |
|||||||||
|
4 |
44 |
|||||||||
|
5 |
55 |
|||||||||
|
6 |
66 |
|||||||||
|
7 |
77 |
|||||||||
|
… |
||||||||||
|
N |
… |
NN |
||||||||
提示
充分投資組合的風險，只受證券之間協(xié)方差的影響，而與各證券本身的方差無關(guān)。
5.相關(guān)結(jié)論
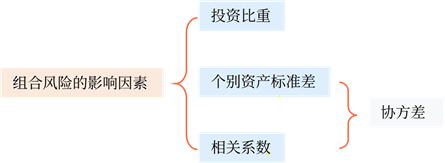
（2）相關(guān)系數(shù)與組合風險之間的關(guān)系
|
相關(guān)系數(shù)r12 |
組合的標準差σp （以兩種證券為例） |
風險分散情況 |
|
r12=1（完全正相關(guān)） |
σp=a+b =比重1σ1+比重2σ2 組合標準差=加權(quán)平均標準差 |
σp達到最大。組合不能抵消任何風險 |
|
r12=-1（完全負相關(guān)） |
σp=|a-b| =|比重1σ1-比重2σ2| |
σp達到最小，甚至可能是零。組合可以最大程度地抵消風險 |
|
r12＜1 |
0＜σp＜加權(quán)平均標準差 |
資產(chǎn)組合可以分散風險，但不能完全消除風險 |
宮老師
2022-06-26 09:58:19 2795人瀏覽
哈嘍！努力學習的小天使：
當相關(guān)系數(shù)ρ1,2=1時，組合標準差公式變?yōu)椋?/span>
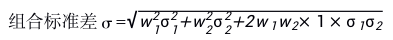
由數(shù)學關(guān)系式a2+b2+2ab=（a+b）2，把w1σ1看做是a，w2σ2看做是b
則該公式變?yōu)椋?/span>
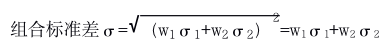
可見相關(guān)系數(shù)為1時，兩者完全正相關(guān)，組合的標準差是組合中各單項資產(chǎn)標準差和比重的加權(quán)平均，故不能分散任何風險。
如果相關(guān)系數(shù)小于1時，則組合標準差會小于加權(quán)平均的標準差，所以可以分散風險。
希望老師的解答能夠?qū)δ袔椭鷡
相關(guān)答疑
-
2024-07-23
-
2020-08-14
-
2020-06-21
-
2020-05-25
-
2020-05-02
您可能感興趣的CPA試題
津公網(wǎng)安備12010202000755號