互换娇妻爽文100系列电影,张娜拉自曝3年300多次,人妻洗澡被强公日日澡电影,妖精漫画免费登录页面入口大全

⑤普通年金終值

A=100、i=10%、n=5

F=A×[(1+i)ⁿ-1]/i

式中[(1+i)ⁿ-1]/i 為年金終值系數(教材附表3)

記作(F/A,i,n);n 為計算利息的期數。

【教材例2-10】2018年1月16日，某人制定了一個存款計劃，計劃從2019年1月16日開始，每年存入銀行10萬元，共計存款5次，最后一次存款時間是2023年1月16日。每次的存款期限都是1年，到期時利息和本金自動續存。假設存款年利率為2%，打算在2024年1月16日取出全部本金和利息。

【分析】本例中，“每次的存款期限是1年，到期時利息和本金自動續存”意味著是“復利按年計息”。所以：

2019年1月16日的10萬元存款在2024年1月16日的本利和=10×(1+2%)⁵

2020年1月16日的10萬元存款在2024年1月16日的本利和=10×(1+2%)⁴

2021年1月16日的10萬元存款在2024年1月16日的本利和=10×(1+2%)³

2022年1月16日的10萬元存款在2024年1月16日的本利和=10×(1+2%)²

2023年1月16日的10萬元存款在2024年1月16日的本利和=10×(1+2%)

在2024年1月16日取出的全部本金和利息

=10×(1+2%)+10×(1+2%)²+10×(1+2%)³+10×(1+2%)⁴+10×(1+2%)⁵

對照普通年金終值的公式

F=A×(F/A,i,n)=A+A(1+i)+A(1+i)²+…+A(1+i)^n-1

可知，本題并不是普通年金終值計算問題。但是可以間接利用普通年金終值計算公式。

由于,

10×(1+2%)+10×(1+2%)²+10×(1+2%)³+10×(1+2%)⁴

+10×(1+2%)⁵=[10+10×(1+2%)+10×(1+2%)²

+10×(1+2%)³+10×(1+2%)⁴]×(1+2%)

所以，在2024年1月16日取出的全部本金和利息=10×(F/A,2%,5)×(1+2%)=10×5.2040×1.02=53.08(萬元)

10×(F/A,2%,5)表示的是在2023年1月16日的全部本金和利息合計。

假設2018年1月16日為0時點，則本題的計算過程可以用圖示表示如下(見圖2-11)。

【例題·單選題】某公司從本年度起每年年末存入銀行一筆固定金額的款項，若按復利計算第n年末可以從銀行取出的本利和，則按最簡便的計算，應選用的時間價值系數是(　　)。

A.復利終值系數

B.復利現值系數

C.普通年金終值系數

D.普通年金現值系數⑥預付年金終值

【答案】C

【解析】利用年金終值公式計算最為簡便。

⑥預付年金終值

【方法一】n=5

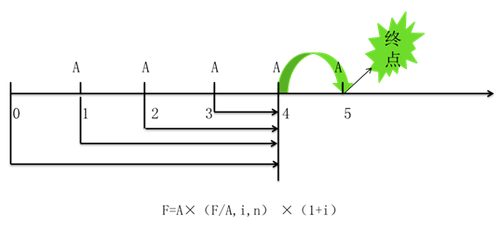
【方法二】n=5

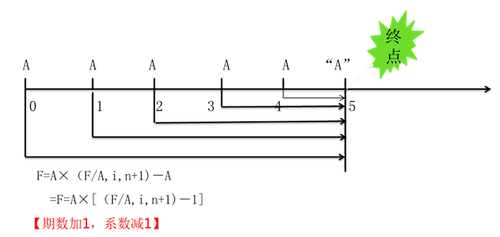
【教材例2-11】2018年1月16日，某人制定了一個存款計劃，計劃從2018年1月16日開始，每年存入銀行10萬元，共計存款5次，最后一次存款時間是2022年1月16日。每次的存款期限都是1年，到期時利息和本金自動續存。假設存款年利率為2%，打算在2023年1月16日取出全部本金和利息。

【分析】

2018年1月16日的10萬元存款在2023年1月16日的本利和=10×(1+2%)⁵

2019年1月16日的10萬元存款在2023年1月16日的本利和=10×(1+2%)⁴

2020年1月16日的10萬元存款在2023年1月16日的本利和=10×(1+2%)³

2021年1月16日的10萬元存款在2023年1月16日的本利和=10×(1+2%)²

2022年1月16日的10萬元存款在2023年1月16日的本利和=10×(1+2%)

在2023年1月16日取出的本部本金和利息

=10×(1+2%)+10×(1+2%)²+10×(1+2%)³+10×(1+2%)⁴+10×(1+2%)⁵

對照預付年金終值F=A×(F/A，i，n)×(1+i)

=A(1+i)+A(1+i)²+……+A(1+i)ⁿ可知：

在2023年1月16日取出的全部本金和利息

=10×(F/A，2%，5)×(1+2%)=10×5.2040×1.02=53.08(萬元)

【提示】如果本題要求計算在2022年1月16日取出的全部本金和利息，則按照10×(F/A,2%,5)計算。

【例題·多選題】下列各項中，其數值等于即付年金終值系數的有(　　)。

A.(P/A，i，n)×(1+i)

B.[(P/A，i，n-1)+1]

C.(F/A，i，n)×(1+i)

D.[(F/A，i，n+1)-1]

【答案】CD

【解析】選項C、D是預付年金終值系數的表達式。

⑦遞延年金終值

(4)年償債基金和年資本回收額

①償債基金的計算

A=F/(F/A，i，n)

償債基金系數1/ (F/A，i，n)

與年金終值系數(F/A，i，n)

互為倒數

【教材例2-13】某家長計劃10年后一次性取出50萬元，作為孩子的出國費用。假設銀行存款年利率為5%，復利計息，該家長計劃1年后開始存款，每年存一次，每次存款數額相同，共計存款10次。

【分析】假設每次存款的數額為A萬元，則有：

A×(F/A，5%，10)=50

A×12.578=50

A=3.98萬元

②資本回收額的計算

A=P/(P/A，i，n)

資本回收系數1/(P/A，i，n)

與年金現值系數(P/A，i，n)

互為倒數

【教材例2-14】某人于20×8年1月25日按揭貸款買房，貸款金額為100萬元，年限為10年，年利率為6%，月利率為0.5%，從20×8年2月25日開始還款，每月還一次，共計還款120次，每次還款的金額相同。

【分析】由于100萬元是現在的價值，所以，本題屬于已知普通年金現值求年金，屬于年資本回收額計算問題。

假設每次還款金額為A萬元，則有：

100=A×(P/A，0.5%，120)

A=100÷(P/A，0.5%，120)

其中(P/A，0.5%，120)的數值無法在教材后面的附表中查到，可以根據(P/A，i，n)的數學表達式用計算器或計算機計算。計算結果

(P/A，0.5%，120)=90.08，所以：

A=100÷90.08=1.11(萬元)

即每月的還款額為1.11萬元。

【例題·單選題】下列各項中，與普通年金終值系數互為倒數的是(　　)。

A.預付年金現值系數

B.普通年金現值系數

C.償債基金系數

D.資本回收系數

【答案】C

【解析】償債基金系數與普通年金終值系數互為倒數，選項C正確。

【例題·多選題】下列關于資金時間價值系數關系的表述中，正確的有(　　)。

A.普通年金現值系數×資本回收系數=1

B.普通年金終值系數×償債基金系數=1

C.普通年金現值系數×(1+折現率)=預付年金現值系數

D.普通年金終值系數×(1+折現率)=預付年金終值系數

【答案】ABCD

【解析】本題考察資金時間價值系數之間的聯系，選項ABCD均正確。

知識點3　利率的計算

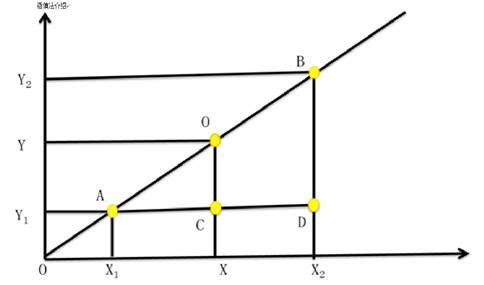
【原理】直線上的三個點任意兩點橫坐標差額之比與對應縱坐標差額之比相等。(相似三角形線性等比關系)

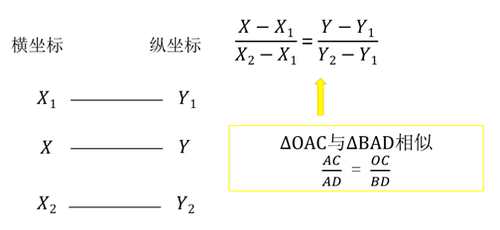
【應用】假設利率與系數、現值、終值存在線性關系

(一)現值或終值系數已知的利率計算

步驟如下：

1.查閱相應的系數表，如果能在系數表中查到相應的數值，則對應的利率就是所求的利率。

2.如果在系數表中無法查到相應的數值，則可以使用內插法(也叫插值法)計算。

假設所求利率為i，i對應的現值(或者終值)系數為B，B₁、B₂為現值(或者終值)系數表中B相鄰的系數，i₁、i₂為B₁、B₂對應的利率。

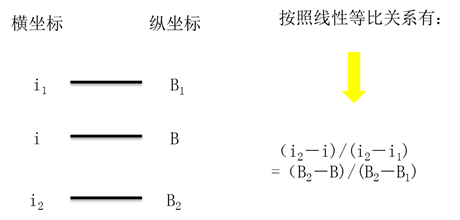
【提示】在寫線性等比關系式時，也可以改變數字順序，只要左右保持對稱(保持參數對應關系)，計算的結果均是正確的。

【教材例2-15】已知(P/F，i，5)=0.7835，求i的數值。

【分析】查閱復利現值系數表可知，在期數為5的情況下，利率為5%的復利現值系數為0.7835，所以，i=5%。