馬爾科夫分析法_25年注冊會計師戰略學習要點
3科
日均>3h
備考注冊會計師戰略科目時，請各位考生以“體系化學習”為導向，避免碎片化記憶。下文整理了戰略科目的知識點馬爾科夫分析法，從概述、適用范圍、優點和局限性帶領考生復習知識點，一起來看！
【所屬章節】
第七章：風險管理的流程、體系與方法
第三節：風險管理的技術與方法
【知 識 點】
馬爾科夫分析法
概述 | ①馬爾科夫分析方法主要圍繞“狀態”這個概念展開。如果系統未來的狀態僅取決于其現在的狀況，那么就可以使用馬爾科夫分析法，這種方法通常用于對那些存在多種狀態（包括各種降級使用狀態）的可維修復雜系統進行分析，更適合于計算機程序 ②馬爾科夫分析法是一項定量技術，它分析的各種狀態可以是不連續的（利用狀態間變化的概率），也可以是連續的（利用各狀態的變化率）。隨機轉移概率矩陣可用來描述狀態間的轉移，以計算各種輸出結果，即各種狀態下的概率 |
適用范圍 | 適用于對復雜系統中的不確定性事件及其狀態改變進行定量分析 |
優點 | 能夠計算出具有維修能力和多重降級狀態的系統的概率 |
局限性 | ①無論是故障還是維修，都假設狀態變化的概率是固定的 ②所有事項在統計上都具有獨立性，因此未來的狀態獨立于一切過去的狀態，除非兩個狀態緊密相接 ③需要了解狀態變化的各種概率 ④有關矩陣運算的知識比較復雜，非專業人士很難看懂 |
點撥：馬爾科夫矩陣
功能、降級和故障將分別界定為狀態S1、狀態S2以及狀態S3。系統每天都存在于這三種狀態中的某一種狀態。下表說明了系統明天處于狀態Si的概率（i可以是1、2或3）。
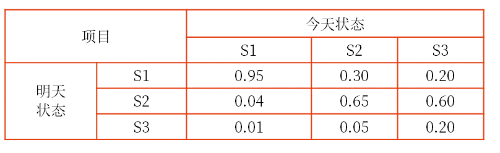
上述概率矩陣稱為馬爾科夫矩陣，或是轉移矩陣。注意，每欄數值之和是1，因為它們是每種情況一切可能結果的總和。
Pi表示系統處于狀態i的概率，根據上述矩陣可以得到如下的方程組：
P1=0.95P1+0.30P2+0.20P3 （1）
P2=0.04P1+0.65P2+0.60P3 （2）
P3=0.01P1+0.05P2+0.20P3 （3）
1=P1+P2+P3 （4）
解聯立方程組可得狀態1、2和3的概率：P1=0.85；P2=0.13；P3=0.02。
● ● ●
以上就是注冊會計師考試《公司戰略與風險管理》科目知識點“馬爾科夫分析法”相關內容，完成上述知識點學習后，考生可以點擊下圖進入免費題庫，開始章節刷題，鞏固基礎，加深印象！
注：以上內容選自肖迪老師注冊會計師《戰略》科目基礎班授課講義
（本文是東奧會計在線原創文章，轉載請注明來自東奧會計在線）
相關文章
津公網安備12010202000755號