金融期權價值的評估方法_2024注會財管備考重點
在學習2024年注會《財管》第六章的“金融期權價值的評估方法”時,閆華紅老師給到考生一處提示:關于一致性原則如果考試給的是年有效利率,期數折算為年折現即可;如果考試給的是報價利率,把報價利率換為期利率,年數換為期數即可。
? 24年注會沖刺階段章節習題,點擊練習 > ? 新人福利領取,登錄即送專屬學習資料!>
注會考試中《財管》科目是學習難度較大的科目。除了要有一定的會計理論基礎支撐之外。還要有一定的理科思維及運算能力。但并不意味著《財管》是難以突破的存在。掌握重點知識,爭取在核心內容上得分,亦是備考的技巧之一。想知道更多《財管》的備考重點。
點擊查看:2024年注會財管《輕一》名師講義,備考重點匯總>>
【所屬章節】
第六章 期權價值評估
第三節 金融期權價值評估
【知 識 點】
金融期權價值的評估方法
(一)期權估值原理
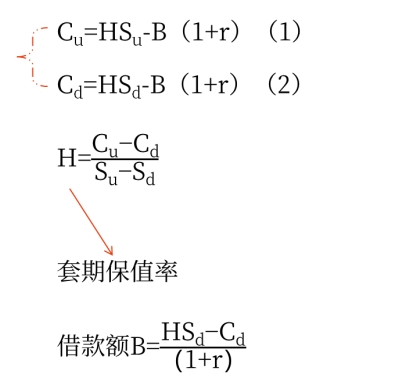
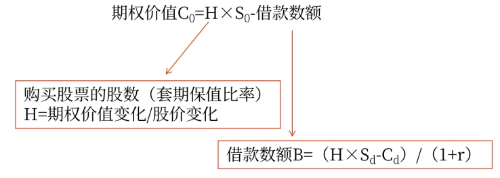
1.復制原理(構造借款買股票的投資組合,作為期權等價物)
(1)基本思想
構造一個股票和借款的適當組合,使得無論股價如何變動,投資組合的損益都與期權相同,那么,創建該投資組合的成本就是期權的價值。
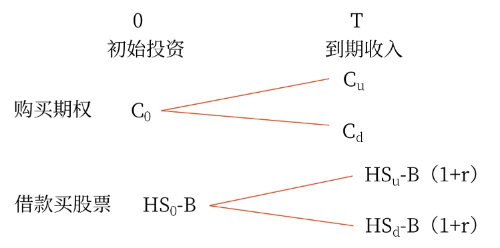
按照套期保值原理,令到期收入相等
(2)計算公式
2.風險中性原理
(1)基本思想
假設投資者對待風險的態度是中性的,所有證券的期望報酬率都應當是無風險利率。
(2)計算思路
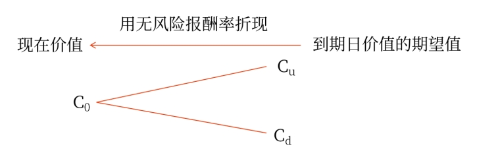
(3)基本公式
到期日價值的期望值=上行概率×Cu+下行概率×Cd
期權價值=到期日價值的期望值÷(1+持有期無風險利率)=(上行概率×Cu+下行概率×Cd)/(1+r)
(4)上行概率的計算
期望報酬率(無風險利率)=上行概率×上行時報酬率+下行概率×下行時報酬率
假設股票不派發紅利,股票價格的上升百分比就是股票投資的報酬率。
期望報酬率(無風險利率)=上行概率×股價上升百分比+下行概率×(-股價下降百分比)
(二)二叉樹期權定價模型
1.單期二叉樹定價模型
期權價格=(1+r-d)/(u-d)×Cu/(1+r)+(u-1-r)/(u-d)×Cd/(1+r)
u:上行乘數=1+上升百分比
d:下行乘數=1-下降百分比
r:無風險的期利率
理解
風險中性原理的應用:
其中:上行概率=(1+r-d)/(u-d)
下行概率=(u-1-r)/(u-d)
期權價格=上行概率×Cu/(1+r)+下行概率×Cd/(1+r)
復制原理的應用:

結論
二叉樹定價模型的公式的推導可以利用復制原理來推導,也可利用風險中性原理來推導。
提示
掌握二叉樹公式時就按風險中性原理來把握即可。
2.兩期二叉樹模型
(1)基本原理:由單期模型向兩期模型的擴展,不過是單期模型的兩次應用。
(2)方法:
先利用單期定價模型,根據Cuu和Cud計算節點Cu的價值,利用Cud和Cdd計算Cd的價值;然后,再次利用單期定價模型,根據Cu和Cd計算C0的價值,從后向前推進。
3.多期二叉樹模型
(1)原理:從原理上看,與兩期模型一樣,從后向前逐級推進,只不過多了一個層次。
(2)股價上升與下降的百分比的確定:
期數增加以后帶來的主要問題是股價上升與下降的百分比如何確定問題。期數增加以后,要調整價格變化的升降幅度,以保證年報酬率的標準差不變。
把年報酬率標準差和升降百分比聯系起來的公式是:

(三)布萊克-斯科爾斯期權定價模型(BS模型)
1.假設
(1)在期權壽命期內,期權標的股票不發放股利,也不做其他分配;
(2)股票或期權的買賣沒有交易成本;
(3)短期的無風險利率是已知的,并且在期權壽命期內保持不變;
(4)任何證券購買者都能以短期的無風險利率借得任何數量的資金;
(5)允許賣空,賣空者將立即得到所賣空股票當天價格的資金;
(6)看漲期權只能在到期日執行;
(7)所有證券交易都是連續發生的,股票價格隨機游走。
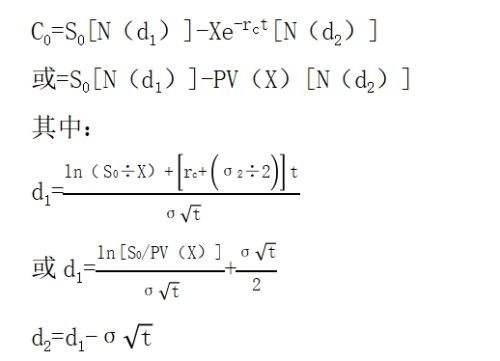
式中: ——看漲期權的當前價值;
![]() ——標的股票的當前價格;
——標的股票的當前價格;
N(d)——標準正態分布中離差小于d的概率;
X——期權的執行價格;
e——自然對數的底數,約等于2.7183;
![]() ——連續復利的年度的無風險報酬率;
——連續復利的年度的無風險報酬率;
t——期權到期日前的時間(年);
In(![]() )——
)——![]() 的自然對數;
的自然對數;
σ2——連續復利的以年計的股票回報率的方差。
附表七 正態分布下的累計概率[N(d)]
X/σ | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
提示
根據d求N(d)的數值時,可以查教材后附的“正態分布下的累積概率[N(d)]”。由于表格的數據是不連續的,有時需要使用插補法計算更準確的數值。當d為負值時,對應的N(d)=1-N(-d),例如N(-0.35)=1-N(0.35)=1-0.6368=0.3632。
3.參數估計
(1)無風險利率的估計
①期限要求:無風險利率應選擇與期權到期日相同的政府債券利率。如果沒有相同時間的,應選擇時間最接近的政府債券利率。
②這里所說的政府債券利率是指其市場利率(根據市場價格計算的到期收益率),而不是票面利率。
③模型中的無風險利率是按連續復利計算的利率,而不是常見的年復利。
連續復利假定利息是連續支付的,利息支付的頻率比每秒1次還要頻繁。
如果用F表示終值,P表示現值,![]() 表示連續復利率,t表示時間(年);則:
表示連續復利率,t表示時間(年);則:
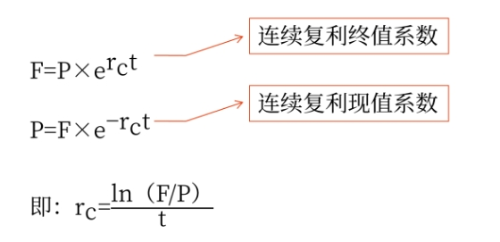
(2)標準差的估計
(3)公式運用
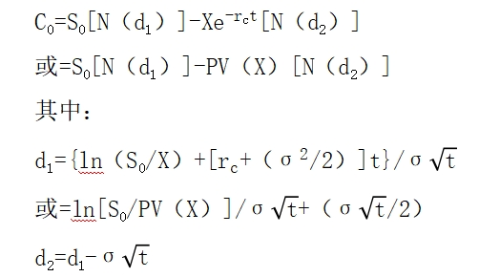

4.看漲期權-看跌期權平價定理
對于歐式期權,假定看漲期權和看跌期權有相同的執行價格和到期日,則下述等式成立:
看漲期權價格-看跌期權價格=標的資產的價格-執行價格的現值
這種關系,被稱為看漲期權-看跌期權平價定理,利用該等式中的4個數據中的3個,就可以求出另外1個。
5.派發股利的期權定價
考慮派發股利的期權定價公式如下:

6.美式期權估值
美式期權在到期前的任意時間都可以執行,除享有歐式期權的全部權利之外,還有提前執行的優勢。因此,美式期權的價值應當至少等于相應歐式期權的價值,在某種情況下比歐式期權的價值更大。
注會考試時間是8月23日-25日,知識學習需要徐徐漸進,掌握重要內容,更會事半功倍。上文知識點內容根據閆華紅老師《輕一基礎精講班》講義整理,閆華紅老師2024年主講的注會C雙名師輕松過關?班課程正在更新!2025年注會新課也已上線,想給自己加一年保障,可點擊圖片了解詳情。
(本文為東奧會計在線原創文章,僅供考生學習使用,禁止任何形式的轉載)
















































 津公網安備12010202000755號
津公網安備12010202000755號