證券資產(chǎn)組合的風險與收益_2020年《財務(wù)與會計》預習考點
上一節(jié)我們一起學習了資產(chǎn)的收益與收益率,通過學習大家已經(jīng)掌握資產(chǎn)收益如何計算了嗎?本節(jié)我們來一起學習稅務(wù)師的新內(nèi)容。
【內(nèi)容導航】
證券資產(chǎn)組合的風險與收益
【所屬章節(jié)】
本知識點屬于《財務(wù)與會計》第二章-財務(wù)管理基礎(chǔ)
【知識點】證券資產(chǎn)組合的風險與收益
證券資產(chǎn)組合的風險與收益
(一)證券資產(chǎn)組合的預期收益率
1.概念
證券資產(chǎn)組合的預期收益率就是組成證券資產(chǎn)組合的各種資產(chǎn)收益率的加權(quán)平均數(shù),其權(quán)數(shù)為各種資產(chǎn)在組合中的價值比例。
2.計算公式
證券資產(chǎn)組合的預期收益率E(Rp)= E(Ri)
式中:E(Rp)表示證券資產(chǎn)組合的預期收益率
E(Ri)表示組合內(nèi)第i項資產(chǎn)的預期收益率
Wi表示第i項資產(chǎn)在整個組合中所占的價值比例
【提示】根據(jù)上述公式,證券資產(chǎn)組合預期收益率的影響因素包括資產(chǎn)價值比例和資產(chǎn)的預期收益率。
【名詞辨析】資產(chǎn)組合、證券組合、市場組合
資產(chǎn)組合 | 指兩個或兩個以上資產(chǎn)所構(gòu)成的集合 |
證券組合 | 如果資產(chǎn)組合中的資產(chǎn)均為有價證券,則該資產(chǎn)組合稱為證券組合(證券資產(chǎn)組合) |
市場組合 | 指由市場上所有資產(chǎn)組成的組合 |
(二)證券資產(chǎn)組合的風險及其衡量
1.證券資產(chǎn)組合的風險分散功能
(1)兩項證券資產(chǎn)組合的收益率的方差:
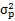 =
=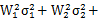 2
2 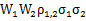
(2)兩項證券資產(chǎn)組合的收益率的標準差:
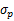 =
= 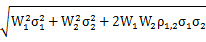
式中: 表示證券資產(chǎn)組合的標準差,它衡量的是組合的風險;
和 分別表示組合中兩項資產(chǎn)的標準差;
和 分別表示組合中兩項資產(chǎn)所占的價值比例;
反映兩項資產(chǎn)收益率的相關(guān)程度,稱為相關(guān)系數(shù)。理論上,相關(guān)系數(shù)介于區(qū)間[-1,1]內(nèi)。
【提示1】根據(jù)上述公式,證券資產(chǎn)組合的收益率的方差(標準差)的影響因素,包括資產(chǎn)價值比例w、資產(chǎn)的標準差σ和相關(guān)系數(shù)ρ。
【提示2】相關(guān)系數(shù)ρ與組合風險之間的關(guān)系
相關(guān)系數(shù) | 含義 | 組合的標準差 | 風險分散功能 |
ρ1,2=1 | 兩項資產(chǎn)的收益率具有完全正相關(guān)的關(guān)系,它們的收益率變化方向和變化幅度完全相同 | σp=w1σ1+w2σ2 σp的值達到最大 | 不能降低任何風險 |
ρ1,2=-1 | 兩項資產(chǎn)的收益率具有完全負相關(guān)的關(guān)系,即它們的收益率變化方向和變化幅度完全相反 | σp=|w1σ1-w2σ2| σp的值達到最小 | 能夠最大限度地降低風險 |
-1<ρ1,2<1 | 具有不完全的相關(guān)關(guān)系 | 0<σp<w1σ1+w2σ2 | 能夠分散風險,但不能完全消除風險 |
2.風險的分類及含義
種類 | 含義 | 與資產(chǎn)組合中資產(chǎn) 個數(shù)之間的關(guān)系 | |
非系統(tǒng)風險 | 又被稱為公司風險或可分散風險,是可以通過證券資產(chǎn)組合而分散掉的風險 | 可通過增加組合中資產(chǎn)個數(shù)而最終消除 | |
經(jīng)營風險 | 指因生產(chǎn)經(jīng)營(供應(yīng)、生產(chǎn)、銷售等)方面的原因給企業(yè)目標帶來不利影響的可能性 | ||
財務(wù)風險 | 又稱籌資風險,是指由于舉債而給企業(yè)目標帶來的可能影響 | ||
系統(tǒng) 風險 | 是影響所有資產(chǎn)的、不能通過資產(chǎn)組合而消除的風險。 影響因素包括宏觀經(jīng)濟形勢的變動、國家經(jīng)濟政策的變化、稅制改革、企業(yè)會計準則改革、世界能源狀況、政治因素等 | 不能通過增加資產(chǎn)組合中的資產(chǎn)個數(shù)而消除,不受資產(chǎn)組合中資產(chǎn)個數(shù)的影響 | |
【提示】證券組合風險與證券組合中的證券資產(chǎn)數(shù)量
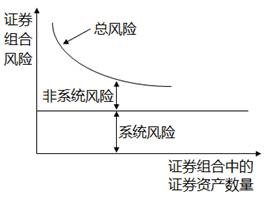
3.系統(tǒng)風險及其衡量
盡管絕大部分企業(yè)和資產(chǎn)都不可避免地受到系統(tǒng)風險的影響,但并不意味著系統(tǒng)風險對所有資產(chǎn)或所有企業(yè)有相同的影響。有些資產(chǎn)受系統(tǒng)風險的影響大一些,而有些資產(chǎn)受系統(tǒng)風險的影響較小。
單項資產(chǎn)或證券資產(chǎn)組合受系統(tǒng)風險影響的程度,可以通過系統(tǒng)風險系數(shù)(β系數(shù))來衡量。
(1)單項資產(chǎn)的系統(tǒng)風險系數(shù)(β系數(shù))
含義 | 單項資產(chǎn)的β系數(shù)是指可以反映單項資產(chǎn)收益率與市場平均收益率之間變動關(guān)系的一個量化指標,它表示單項資產(chǎn)收益率的變動受市場平均收益率變動的影響程度。 |
計算公式 | 指標說明: ①ρi,m表示該項資產(chǎn)的收益率與市場組合收益率的相關(guān)系數(shù); ②σi表示該項資產(chǎn)收益率的標準差,反映該資產(chǎn)的風險大小; ③σm表示市場組合收益率的標準差,反映市場組合的風險; ④COV(Ri,Rm)表示該資產(chǎn)收益率與市場組合收益率的協(xié)方差。 COV(Ri,Rm)=ρi.mσiσm 【提示1】根據(jù)COV(Ri,Rm)=ρi.mσiσm,則: ρi,m=COV(Ri,Rm)/(σiσm) 【提示2】根據(jù)公式,當相關(guān)系數(shù)ρ小于零時,β系數(shù)小于零。 |
結(jié)論 | ①當某資產(chǎn)的β系數(shù)絕對值=1,說明該資產(chǎn)的收益率與市場平均收益率成同比例的變化,該資產(chǎn)所含的系統(tǒng)風險與市場組合的風險一致; ②當某資產(chǎn)的β系數(shù)絕對值<1,說明該資產(chǎn)收益率的變動幅度小于市場組合收益率的變動幅度,因此其所含的系統(tǒng)風險小于市場組合的風險; ③當某資產(chǎn)的β系數(shù)絕對值>1,說明該資產(chǎn)收益率的變動幅度大于市場組合收益率的變動幅度,因此其所含的系統(tǒng)風險大于市場組合風險。 |
【提示】市場組合是指由市場上所有資產(chǎn)組成的組合。
(1)市場組合收益率就是市場平均收益率,實務(wù)中通常用股票價格指數(shù)的收益率來代替;
(2)市場組合收益率的方差則代表了市場整體的風險。由于包含了所有的資產(chǎn),市場組合中的非系統(tǒng)風險已經(jīng)被消除,所以市場組合的風險就是市場風險或系統(tǒng)風險。
(3)證券資產(chǎn)組合的系統(tǒng)風險系數(shù)
含義 | 證券資產(chǎn)組合的β系數(shù)是所有單項資產(chǎn)β系數(shù)的加權(quán)平均數(shù),權(quán)數(shù)為各種資產(chǎn)在證券資產(chǎn)組合中所占的價值比例。 |
計算 公式 | βP=∑Wiβi 指標說明:βP表示證券資產(chǎn)組合的風險系數(shù); Wi表示第i項資產(chǎn)在組合中所占的價值比重; βi表示第i項資產(chǎn)的β系數(shù)。 |
應(yīng)用 | 由于單項資產(chǎn)的β系數(shù)不盡相同,因此通過替換資產(chǎn)組合中的資產(chǎn)或改變不同資產(chǎn)在組合中的價值比例,可以改變組合的風險特性。 |
【小結(jié)】系統(tǒng)風險的衡量指標(β系數(shù))的確定
項目 | β系數(shù)的確定 |
單項資產(chǎn) |
|
無風險資產(chǎn) | β系數(shù)=0 |
證券組合 | βP=∑Wiβi |
市場組合 | β系數(shù)=1 |
本節(jié)稅務(wù)師考試的考點內(nèi)容就到這里,下節(jié)再見。
(注:以上內(nèi)容選自丁奎山老師《財務(wù)與會計》授課講義)
(本文為東奧會計在線原創(chuàng)文章,僅供考生學習使用,禁止任何形式的轉(zhuǎn)載)




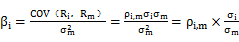
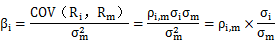




































 津公網(wǎng)安備12010202000755號
津公網(wǎng)安備12010202000755號