2017中級經濟師《金融》基礎考點:現值與終值
2017中級經濟師備考正在緊張而忙碌的進行當中,東奧小編為大家整理了中級經濟師金融知識點:現值與終值
【內容導航】
(一)系列現金流的現值
(二)連續復利下的現值
【所屬章節】:
本知識點屬于《金融》科目第二章 利率與金融資產定價 第一節 利率的計算
【知識點】:現值與終值
現值(Present Value),又稱在用價值,現值是現在和將來(或過去)的一筆支付或支付流在今天的價值。
(一)系列現金流的現值
假如我們有一系列的現金流,第一年年末是100,第二年末是200,第三年年末是200,第四年年末是300,若貼現率為8%,這一系列現金流的現值可以通過每筆資金現金現值的加總得到。
第一年末收入100的現值:100÷(1+8%)=92.59
第二年末收入200的現值:200÷(1+8%)2=171.47
第三年末收入200的現值:200÷(1+8%)3=158.77
第四年末收入300的現值:300÷(1+8%)4=220.51
總現值:643.34
一般地,系列現金流的現值可由下面的公式得到:
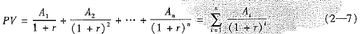
其中,Ai表示第i年末的現金流量,r是年帖現率。
(二)連續復利下的現值
假如一年之內多次支付利息,則利息率為r/m,此時現值的計算公式為:

其中,An表示第n年末的現金流量,m是年計息次數,R是貼現率。假定三年后可能收到100元,貼現率為8%,如果按一季度計息一次計算,則其現值為:

上式中,如果m趨于∞,則
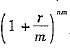
趨于em,因此,如果是連續復利,那么現值的計算公式為:
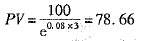
假定三年后可以收到100元,貼現率為8%,且若連續復利,則其現值為:
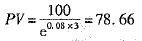
每年的計息次數越多,現值越小,隨計息間隔的縮短,現值以遞減的速度減小,最后等于連續復利條件下的現值。
(三)終值及其計算
終值(Future Value),又稱將來值或本息和,是指現在在一定量的資金在未來某一時間點上的,價值。終值的大小不僅取決于現值的大小,而且與利率的高低、借款期限和計息方式有關。
終值的計算有兩種方式:單利和復利。
假如當前有一筆資金,共計金額為P,存期為n年,年利率為r,如果按單利計算,則n年后
的終值FVn為:
FVn=P+P·r·n=P(1+r·n) (2一10)
例如,王先生最近購買彩票,中獎1萬元,他想將這筆錢存人銀行,以便將來退休時用,設王先生還有10年退休,如按單利計算,年存款利率為4%,那么10年后王先生退休時能拿到多少錢?
如果按單利計算,王先生退休時能拿的本息和為10 000×(1 +4%×10)=14 000元。
假設當前有一筆資金,共計金額為P,薦期為n年,年利率為r,如果每年復利一次,則n年后的終值FVn為:
第1年年來的本息和為P(1+r)
第2年年末的本息和為P(1+r)(1+r)=P(1+r)2
第3年年末的本息和為P(1+r)2(1+r)=P(1+r)3
…
第n年年末的本息和為P(1+r)n
因此,FVn=P(1+r)n,其中(1+r)n稱為復利終值系數。
上例中,如果按復利計算,則王先生10年后可獲得:
10 000×(1+4%)10=14 802.44元
更多練習題可以查看中級經濟師每日一練匯總
(本文是東奧會計在線原創文章,轉載請注明來自東奧會計在線)

































 津公網安備12010202000755號
津公網安備12010202000755號