東奧名師講解貨幣時間價值,“錢都去哪了?”
2018年東奧重磅打造屬于財會人的知識盛宴——“財會狂歡節”正如火如荼的進行中。中級會計職稱《財務管理》一直以來都以“公式多”“難記憶”號稱,其中貨幣時間價值作為需要考生重點掌握的章節,讓我們看一看如何用舉例的方式讓大家深透理解貨幣時間價值的吧!
貨幣時間價值、現值、終值、年金的含義
打個比方,如果你的老板答應你如果今年拿到中級會計證書就加薪,但是薪水的支付方式有三種:①年初一次性支付24萬;②每月支付2萬;③年末一次性支付24萬。你會選擇哪一種呢?
這三種選擇看似結果好像是一樣的,但是在學完貨幣時間價值以后,大家就會發現它們的不同了。
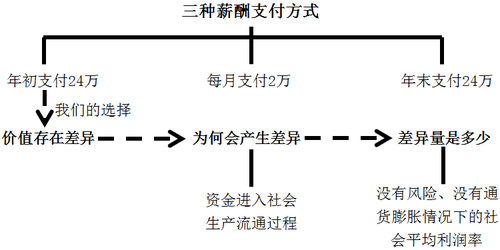
在加薪支付方式的三種選擇中,大家多數會憑直覺選擇第一種,也就是希望公司在年初一次性支付24萬。大家的這個選擇確實會和另兩種選擇的結果在價值上產生差異,至于為什么會產生差異呢?是因為資金進入社會生產流通過程中,隨著時間的推移,會產生差異量。
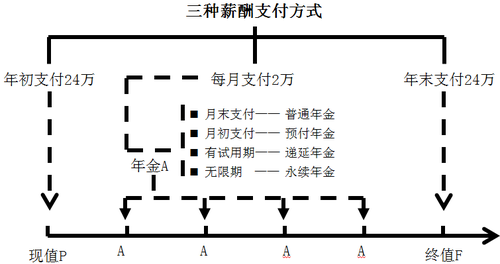
如果選擇2018年年初來支付的話:年初支付的24萬就是現值,年末支付的24萬就是終值,而每月支付2萬就是年金。但是大家再來假設一下,如果你的老板在如何支付這每月2萬的問題上再給你四個選擇---①每月月末支付2萬,這2萬就是普通年金;②每月月初支付2萬,這2萬就是預付年金;③如果老板說拿下中級證書以后還要再考查你幾個月再開始每月支付2萬,這2萬就是遞延年金;④如果老板說拿下中級證書以后每月支付2萬,一直發到天荒地老,這2萬就是永續年金。
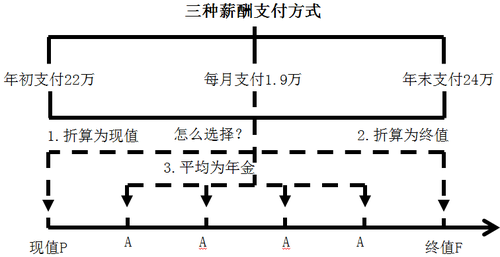
在實際生活中,可能不會像之前舉的例子一樣這么簡化,多數會是年初支付、年金和年末支付數額不同,舉個例子:大家今年要考中級,你的老板答應你如果今年拿到中級證書就加薪,但是薪水的支付方式有三種:①年初一次性支付22萬;②每月支付1.9萬;③年末一次性支付24萬。那么到底哪種方式能獲得更多薪水呢,我們需要把這三種方式折算到統一標準,才好做出判斷,而怎么折算就是貨幣時間價值這章需要大家了解的內容。
現值與終值的相關計算與應用
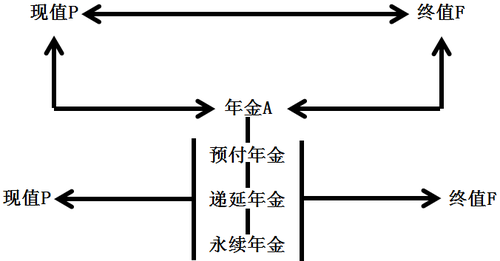
現值與終值的相關計算與應用 在貨幣時間價值這章的邏輯框架為:現值P、年金A(包括預付年金、遞延年金和永續年金)以及終值F之間的轉換。
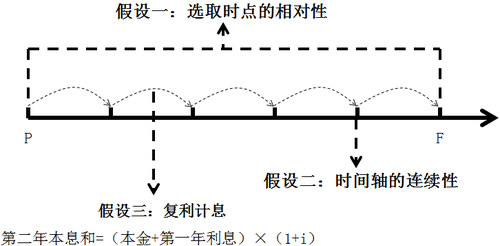
在進行上述轉換前,我們需要做出計算的假設:①選取時間點的相對性,選擇時間點的不同,看現值和終值的角度就不同;②時間軸的連續性,每期期初就是上期期末;③復利計息,也就是俗稱的利滾利。那在用舉例的方式理解一下現值與終值的相關計算與應用。
① 現值到終值的計算
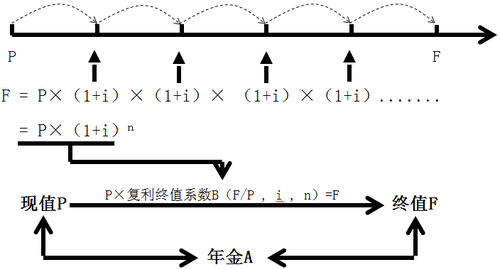
現值P,一期一期向后折現,每期利率是i,一共n期,那么終值F=P×(1+i)n
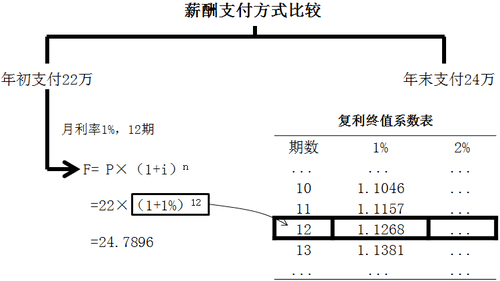
應用:像上述例子中,年初支付22萬,每月利率1%,共12期,那么它的終值=22×(1+1%)12=24.7896,大家看到(1+1%)12可能會覺得計算起來特別復雜,這一點的話大家不用擔心,因為教材最后會附上復利終值系數表,大家依據該表就可以輕松得到(1+1%)12的數值了。
② 終值到現值的計算
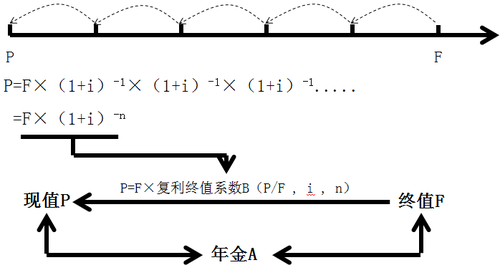
終值F,一期一期向前折現,每期利率是i,一共n期,那么現值P=F×(1+i)-n
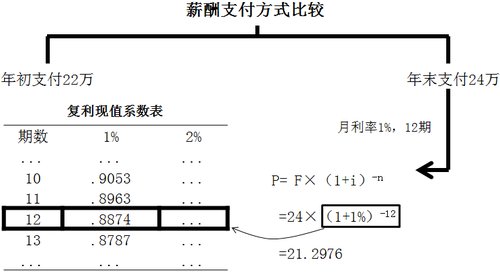
應用:年末支付24萬,每月利率1%,共12期,那么它的現值=24×(1+1%)-12=21.2976。
③ 年金終值FA的計算
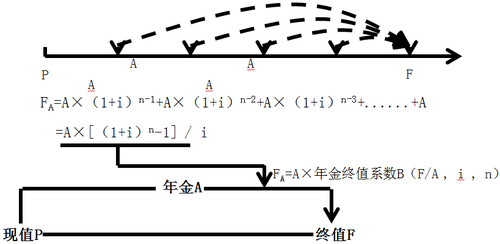
年金A,一期一期向后折現,每期利率是i,一共n期,第一期的年金A向后折現,期限是(n-1)期,即A×(1+i)n-1,以此類推,那么年金終值FA=A×[(1+i)n-1]/i

應用:每月支付1.9萬,每月利率1%,共12期,那么它的年金終值=1.9×[(1+1%)12-1]/1% =24.0977。
④ 年金現值PA的計算
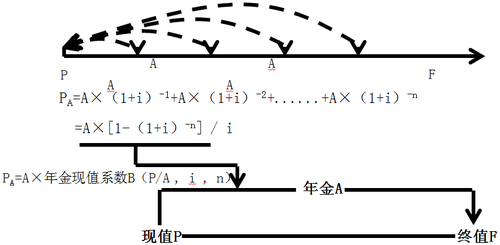
年金A,一期一期向前折現,每期利率是i,一共n期,第一期的年金A向前折現,期限是1期,即A×(1+i)-1,以此類推,那么年金現值PA=A×[1-(1+i)-n]/i

應用:每月支付1.9萬,每月利率1%,共12期,那么它的年金現值=1.9×[1-(1+1%)-12]/1%=21.38469。
在計算過程中我們會發現有四個系數,面對如此相似的公式與計算,我們應該如何記憶呢?通過總結規律給出了以下記憶方法:
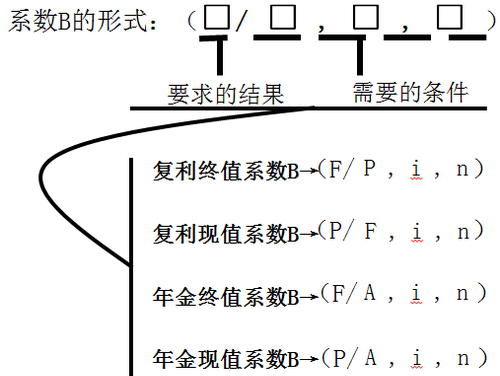
首先括號中的第一個字母代表的含義是下一步要求什么,比方說要求復利終值,那么就是F,要求復利現值,那么就是P。接下來的三個字母代表的是需要的條件,比方說在求復利終值后,我們需要利用到現值、利率、期數求終值。
相信通過老師的講解,大家已經了解了現值與終值之間的轉換,也了解了現值、終值分別與普通年金之間的轉換,至于現值、終值分別與預付年金、遞延年金以及永續年金之間的轉換,大家可以通過正式課程來觀看。
更多名師講解干貨歡迎查看:名師解析中級會計報名,希望大家能在2018年中級會計職稱考試中,一路披荊斬棘,收獲佳績。最后,提醒大家持續收看我們“財會狂歡節”的后續的相關活動,更多干貨內容將為您傾情奉獻!










































 津公網安備12010202000755號
津公網安備12010202000755號