證券資產組合的風險與收益_2021年中級會計財務管理必備知識點

來源：東奧會計在線責編：cyw2021-03-30 10:47:24

只要持之以恒，知識積累豐富，終能發現其中的奧秘。2021年中級會計《財務管理》相關知識點已更新，快和小編一起開啟2021年的備考之路吧！

點擊查看：2021年中級會計《財務管理》必備考點集結！火速收藏！

2021年中級會計財務管理必備知識點

【內容導航】

證券資產組合的風險與收益

【所屬章節】

第二章　財務管理基礎

【知識點】證券資產組合的風險與收益

證券資產組合的風險與收益

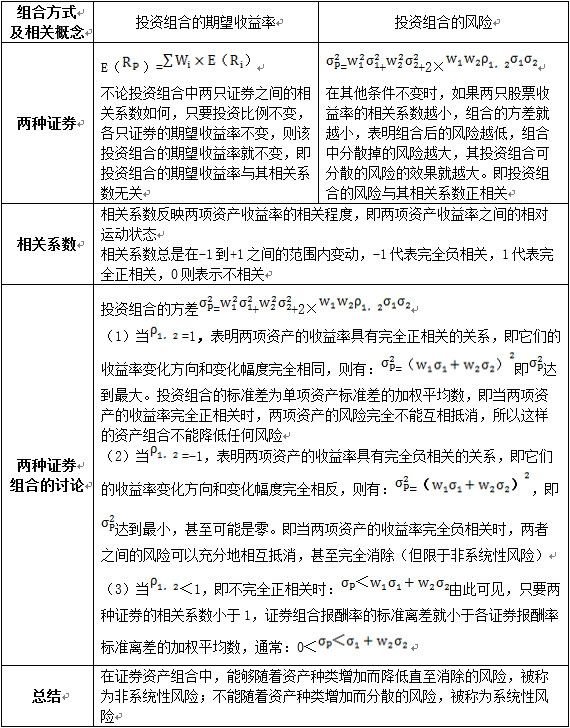
(一)兩項資產組合的風險與收益

兩個或兩個以上資產所構成的集合，稱為資產組合。如果資產組合中的資產均為有價證券，則該資產組合也可稱為證券組合。

微信截圖_20210330103750

(二)風險類別

項目

內容

含義

要點闡釋

風險

類別

非系統風險

是指發生于個別公司的特有事件造成的風險

它只影響一個或少數公司，不會對整個市場產生太大影響。由于非系統風險是個別公司或個別資產所特有的，因此也稱“特殊風險”或“特有風險”。由于非系統風險可以通過資產組合分散掉，因此也稱“可分散風險”

風險

類別

系統

風險

系統風險又被稱為市場風險或不可分散風險，是影響所有資產的、不能通過資產組合來消除的風險

這部分風險是由那些影響整個市場的風險因素所引起的，這些因素包括宏觀經濟形勢的變動、國家經濟政策的變化、稅制改革、企業會計準則改革、世界能源狀況、政治因素等

【提示】在風險分散的過程中，不應當過分夸大資產多樣性和資產個數的作用。實際上，在證券資產組合中資產數目較低時，增加資產的個數，分散風險的效應會比較明顯，但資產數目增加到一定程度時，風險分散的效應就會逐漸減弱。經驗數據表明，組合中不同行業的資產個數達到20個時，絕大多數非系統風險均已被消除掉。此時，如果繼續增加資產數目，對分散風險已經沒有多大的實際意義，只會增加管理成本。另外不要指望通過資產多樣化達到完全消除風險的目的，因為系統風險是不能夠通過風險的分散來消除的。

(三)系統性風險的衡量

		要點闡釋
資產的β系數	含義	某資產的β系數表達的含義是該資產的系統風險相當于市場組合系統風險的倍數
資產的β系數	功能	不同資產的系統風險不同，為了對系統風險進行量化，用β系數衡量系統風險的大小
單項資產的 β系數	經濟含義	當β=1時，表示該單項資產的收益率與市場平均收益率呈相同方向、相同比例的變化，其系統風險與市場組合的風險情況一致；如果β＞1，說明該單項資產的系統風險大于整個市場組合的風險；如果β＜1，說明該單項資產的系統風險小于整個市場組合的風險絕大多數資產的β系數是大于零的，也就是說，它們收益率的變化方向與市場平均收益率的變化方向是一致的，只是變化幅度不同而導致β系數的不同；極個別資產的β系數是負數，表明這類資產與市場平均收益率的變化方向相反，當市場平均收益率增加時，這類資產的收益率卻在減少
投資組合的β系數	含義	投資組合的β系數是所有單項資產β系數的加權平均數，權數為各種資產在投資組合中所占的價值比例
	功能	對于投資組合來說，其系統性風險程度也可以用β系數來衡量
	計算公式	βP=×βi）投資組合的β系數受到單項資產的β系數和各種資產在投資組合中所占比重兩個因素的影響或：βP=E（RP）/（Rm-Rf）該公式適用于在已知投資組合的風險收益率E（RP），市場組合的平均收益率Rm和無風險收益率Rf的基礎上可以推導出特定投資組合的β系數
	調整	由于單項資產的β系數不盡相同，因此通過替換資產組合中的資產或改變不同資產在組合中的價值比例，可以改變資產組合的風險特性