不提前學會這個知識,備考注會《會計》恐要面臨卡頓!
注冊會計師因其報名條件未限制所學專業與工作經驗。因此備考注會的考生中有相當一部分人是沒有財稅基礎的“注會小白”。在學習注會時首要面臨的就是專業壁壘和科目原理的難題。首次備戰注會的財會零基礎考生,學習注會《會計》先別著急一開始就直奔重難點。有一些知識需要提前了解、掌握,才能讓后續章節的學習更加順利。

在注會《會計》中,有一類知識點不是財稅的起步理論概念,但卻是十分重要的知識支撐,東奧張志鳳老師、張敬富老師都曾在學習指導之初,便提醒考生要先為自己的科目學習打下知識基礎。其中“貨幣時間價值”是兩位老師都曾重點提到的。
那么“貨幣時間價值”到底是怎樣的內容呢?我們根據張敬富老師在“巧學基礎班”的講義進行梳理,為考生們提煉出知識精髓。大家一起了解熟悉一下吧。

在注會《會計》科目中,后續的很多章節比如:固定資產、分期付款、租賃等內容,都需要用到終值和現值的概念和計算。因此,在學習上述章節之前,先熟練掌握“時間貨幣價值”就會在備考重要章節時更加得心應手,事半功倍。
終值 (Future Value) | 又稱將來值,是現在一定量的貨幣折算到未來某一時點所對應的金額,通常記作F。(本利和) |
現值 (Present Value) | 是指未來某一時點上一定量的貨幣折算到現在所對應的金額,通常記作P。(本金) |
在注會學習中,“現值”是同學們需要著重掌握的知識點。即已知終值F、利率i、期數n,計算出現值P。因現值與終值互為倒數,所以,只要掌握了正、反雙向的計算過程就可以很好地習得“終值和現值”考點。我們通過下圖來進行簡化理解和演示公式的推導。
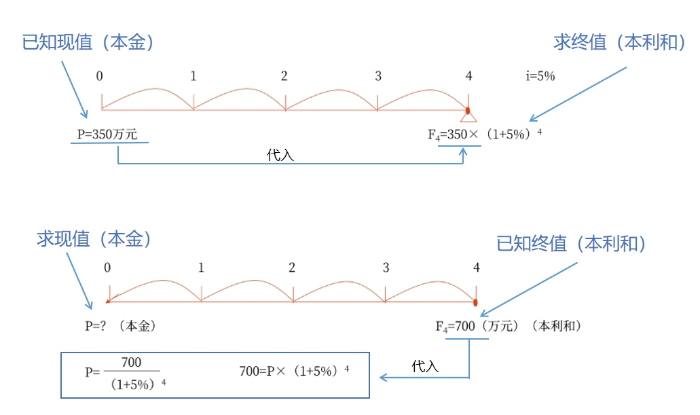
由上圖可知:已知現值求終值,用乘法。公式為Fn=P×(1+i)n
> > > > 提示
上文公式中的n是期數,此時的n可以通過“數格子”來確定,即中間有幾個格,n就為幾。這與下方的“年金”要做好區分。請先記住現值、終值“數格子”的方法。

計息計算有兩種方法,分為“單利”和“復利”。我們以表格形式與將兩個概念進行對比與區分。
單利計息 | 只對本金計算利息,各期利息相等 |
復利計息 | 既對本金計算利息,也對前期的利息計算利息,各期利息不同。 |
通俗解釋一下:假設每一期到期都未將本金與產生的利息取出,而是將“本利和”全部作為下一期的本金再計息,那么當期的利息都會高于上一期的利息,所謂的“利滾利”,這就是“復利”的形式。
舉例說明,設:第一期本金為P=100萬,利息i=10%,那么年初存款到第一年年末,得到的第一年的終值(本利和)F=100*(1+10%)=110萬;假設是復利形式。則本利和不取出,直接當成下一期的本金,假定利率依舊是10%的情況下。那么到第二年年末的終值F=110*(1+10%)=121萬;兩期產生的利息對比,第一期是10萬,低于第二期的利息11萬。以此類推,一直往復下去,產生的利息是越來越高的。這就是復利。
> > > > 提示
“復利”是需要同學們熟練掌握的。因為會涉及到后面的較重點內容——復利現值。同時,在復利里,我們依然要結合現值、終值的圖解,以“數格子”來確定計息期數。

上文我們總結出,終值:F=P×(1+i)n;現值P=F/(1+i)n。隨著期數n的增加,計算量也會變得越來越龐大。因此,會計中將終值公式中的(1+i)n稱為復利終值系數,記為(F/P,i,n)。將現值公式中的1/(1+i)n稱為復利現值系數,記為(P/F,i,n)。在計算時,只需要在系數表格中,找到i對應的列,n對應的行,交匯的數字可以直接代入公式中計算,直接簡化了一步步的累期計算量。
> > > > 提示
記憶小技巧:在系數中,求哪個量,哪了量就在系數的最前面,即(F/P,i,n),F在P之前,這就是求復利終值F。求F,F就在前面。此時要對應去找復利終值系數的表,進行計算。同樣的道理,(P/F,i,n)就是求復利現值P,要在復利現值系數表中,找到對應的數字代入公式。

年金:一定時期內每隔相等時間發生相等金額的收付款項。(等額、同向、同距)。分為:普通年金、預付年金、遞延年金。其中,普通年金是其他年金的基礎,也是學習時需要重點掌握的內容。我們可以用一組圖示大致區別一下各年金的特點。

圖中明顯標注了三類年金的不同之處。數軸上的1-4代表的是一期的期末,即按年計算的話,1代表的是第一年的年末,2代表的是第二年的年末,以此類推。
> > > > 提示
與復利期數的算法“數格子”不同,普通年金的期數n,采取的是“數個數”。即數軸上1-4,一共四個數,那么年金期數n=4。

普通年金現值與復利現值都是需要同學們理解掌握的,計算時兩個公式也比較相似,同樣擁有系數。查詢時一定要認真區分。普通年金的計算公式:

> > > > 提示
在計算時,難度并沒有太大,我們通過一個例子來演算一下。以下圖為例,已知利率i=4%,每期年金A=70萬,求普通年金現值P。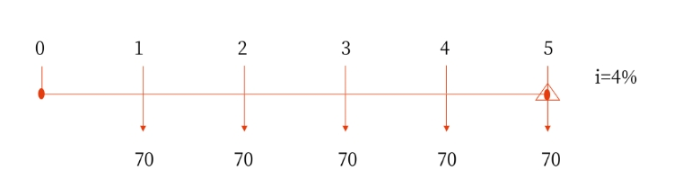
在整個公式中,我們已知條件很齊備,考驗我們的是期數如何確定,年金要以“數個數”的方式,1-5共5個數,因此期數n=5。則普通年金現值系數應該是(P/A,4%,5),假設這個系數查表得出為2.3。那么此題的PA=70*2.3=161就是最后的結果。
綜上,在學習注會《會計》科目之初,我們需要先了解掌握現值、終值、復利、復利現值、普通年金、普通年金現值等概念與計算。從本文中遞進下來的內容來看,并沒有太大的難度,只要理解了方式方法,同學們是可以輕松攻克的。
2024年注會考試新課已經開課,想要更詳細的學習注會基礎內容,歡迎同學們點擊了解。希望通過本文的梳理,可以讓大家克服對注會知識的恐懼,輕松備考,快樂學習。
延伸閱讀:
(本文是東奧會計在線原創文章,轉載請注明來自東奧會計在線)














































 津公網安備12010202000755號
津公網安備12010202000755號