貨幣時間價值_2020年《財務與會計》預習考點
上一節我們在《財務與會計》知識點財務管理環境中結束了第一章的學習,接下來我們學習稅務師科目《財務與會計》的貨幣時間價值。
【內容導航】
貨幣時間價值
【所屬章節】
本知識點屬于《財務與會計》第二章-財務管理基礎
【知識點】貨幣時間價值
貨幣時間價值
一、貨幣時間價值的含義
1.貨幣時間價值,是指一定量貨幣資本在不同時點上的價值量差額。
2.貨幣的時間價值來源于貨幣進入社會再生產過程后的價值增值。通常情況下,它是指沒有風險也沒有通貨膨脹情況下的社會平均利潤率,是利潤平均化規律發生作用的結果。
【解釋】“貨幣的時間價值來源于貨幣進入社會再生產過程后的價值增值”:貨幣進入社會再生產過程后的價值增值不僅包括時間價值,還包括貨幣資金提供者要求的風險報酬率和通貨膨脹補償率,因此價值增值不能等同于貨幣時間價值。
【鏈接】純利率是指沒有風險、沒有通貨膨脹條件下的平均利率。
即,純利率=貨幣時間價值。(教材P10)
二、終值和現值的計算
(一)相關概念
1.終值
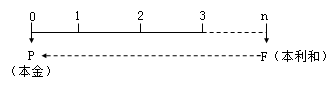
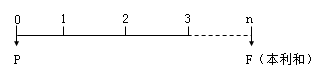
終值又稱將來值,是現在一定量的貨幣折算到未來某一時點所對應的金額,通常用字母“F”表示。

2.現值
現值,是指未來某一時點上一定量的貨幣折算到現在所對應的金額,通常用字母“P”表示。
3.計算利息的期數
現值和終值對應的時點之間可以劃分為n期(n≥1),相當于計息期。相鄰兩次計息的間隔,如年、月、日等,除非特別說明,計息期一般為1年。通常用字母“n”表示。
4.利率
利率為貨幣時間價值的一種具體表現,也稱為折現率。通常用字母“i”表示。利息用字母“I”表示。
5.年金
年金是指間隔期相等的系列等額收付款,通常用字母“A”表示。
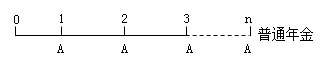
6.計息方式
(1)單利:按照固定的本金計算利息的一種計息方式,所生利息均不加入本金重復計算利息。
(2)復利:不僅對本金計算利息,還對利息計算利息的一種計息方式。
【提示】年金屬于復利的簡便計算方法,不屬于計息方式。
【補充】根據經濟人假設,人們都是理性的,會用賺取的收益進行再投資,企業的資金使用也是如此。因此,財務估值中一般都按照復利方式計算貨幣的時間價值。
(二)復利的終值和現值
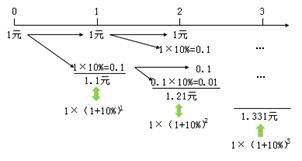
1.復利終值
復利終值指一定量的貨幣,按復利計算的若干期后的本利總和。
現在的1元錢,年利率為10%,從第1年到第5年,各年年末的終值計算如下:

2.復利現值
復利現值是指未來某期的一定量的貨幣,按復利計算的現在價值。
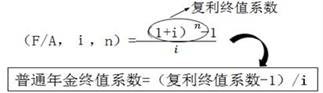
F=P×(1+i)n
P=F×(1+i)-n=F×(P/F,i,n)
復利現值=復利終值×復利現值系數
式中:(1+i)-n、(P/F,i,n)為復利現值系數
【提示1】復利終值和復利現值互為逆運算。
【提示2】復利終值系數和復利現值系數互為倒數。
(1+i)n×(1+i)-n=1
(F/P,i,n)×(P/F,i,n)=1
復利現值系數×復利終值系數=1
(三)普通年金
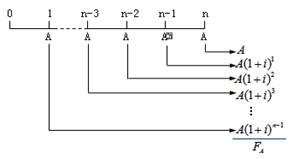
普通年金是年金的最基本形式,是指從第一期起,在一定時期內每期期末等額收付的系列款項。

圖中:A—年金
n—計息期數(年金A發生的次數)
1.普通年金終值
普通年金終值是指普通年金最后一次收付時的本利和,它是每次收付款項的復利終值之和。(已知年金A,求
終值FA)

2.普通年金現值
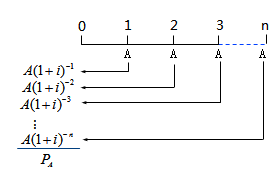
普通年金現值是指將一定時期內按相同時間間隔在每期期末收付的相等金額折算到第一期期初的現值之和。(已知年金A,求現值PA)

【提示1】普通年金終值系數與復利終值系數
【提示2】普通年金現值系數與復利現值系數

本節內容可能有些專業為會計的同學在學校就有學過,因此沒有學過的同學還是要多多練習才能了解稅務師考試中的考點。
(注:以上內容選自丁奎山老師《財務與會計》授課講義)
(本文為東奧會計在線原創文章,僅供考生學習使用,禁止任何形式的轉載)








































 津公網安備12010202000755號
津公網安備12010202000755號